Storia e tecnologie sottostanti: Byzantine General Problem e Merkle Tree

Con questo articolo concludiamo l’introduzione alla tecnologia blockchain andando ad analizzare un po’ più nel dettaglio alcuni dei componenti sottostanti: il problema dei generali bizantini infatti verte sulle modalità di raggiungimento del consenso in ambienti ostili, quindi mira a rafforzare la sicurezza del sistema. Dall’altro lato i merkle tree aiutano ad ottimizzare la velocità di ricerca e validazione delle transazioni.

Byzantine general problem

Uno dei principali problemi nelle comunicazioni a distanza è la debolezza del mezzo di trasmissivo utilizzato. Il problema maggiore è quello di raggiungere il consenso tra le parti attraverso comunicazioni in ambienti che possono subire perdita o corruzione delle informazioni trasmesse.

Nella letteratura esso è conosciuto come Byzantine general problem oppure come Problema dei generali bizantini (o dei due eserciti).

L’esemplificazione classica descrive la situazione in cui 2 o più generali devono coordinare un attacco ad una città ma si trovano ai lati opposti della stessa. La comunicazione avviene tramite messaggeri che fanno la spola tra i due schieramenti. Se ad esempio un generale invia un messaggero per sincronizzare un attacco, lo stesso potrebbe essere catturato dalla città assediata: in tale caso sarebbero possibili 2 scenari:

• il messaggio andrebbe perso
• il messaggio potrebbe essere alterato e spedito all’altro generale: in questo modo le informazioni tra i due schieramenti sarebbero discordanti, a tutto vantaggio della città assediata

Nelle criptovalute e nei sistemi blockchain, la soluzione a questo problema è quella di rendere l’intero ecosistema Trustless. Nessuno dei componenti deve fidarsi dell’altro, non c’è bisogno di dare fiducia a nessuna entità del sistema e si dà per scontato che non ci sia verità e trasparenza in nessun punto.

Il problema dell’alterazione dei messaggi, si risolve quindi con l’introduzione di un nuovo concetto definito Proof of Work (sinteticamente scritto PoW e tradotto Prova di Lavoro). 

Questo prevede la crittazione del messaggio secondo un algoritmo predefinito (ex. SHA256, KECCAK, ecc.) per ottenere un risultato che sia difficile da trovare ma allo stesso tempo, estremamente semplice da verificare.

Un esempio pratico di come funziona il sistema può essere il seguente:

1. Il generale A scrive il messaggio “Attaccare alle 6.00!”
2. Una regola decisa preventivamente impone che il messaggio criptato debba iniziare con “0000”
3. Il generale A concatena un numero chiamato Nonce al messaggio, ottenendo “Attaccare alle 6.00!”.
   Per ora ci basta sapere che il Nonce è un numero casuale che viene utilizzato durante il processo di mining per aiutare a trovare l’hash corretta di un blocco. Entreremo più in dettaglio nei prossimi articoli quando descriveremo il processo di mining.
4. Esegue l’algoritmo SHA256 incrementando di volta in volta il nonce di 1 fino ad ottenere un hash che inizi con i 4 zeri come da accordi. Dopo molte iterazioni di calcolo, ottiene l’hash 

000031612efe654d8fb3194cbb17013d6057ec7fae3f083c27d3788fc8bb5054 

utilizzando il valore di 102654 per il nonce. Questo vuol dire che sono state necessarie 102654 iterazioni di codifica per trovare il nonce che soddisfi il prerequisito iniziale, ossia un hash che inizi con “0000”

5. Al generale B viene trasmesso il messaggio “Attaccare alle 6.00!” e il valore del nonce, 102654
6. Il generale B effettua lo SHA256 dell’intera espressione “Attaccare alle 6.00!102654” e verifica che l’hash calcolato inizia effettivamente con “0000”. Questo assicura che il messaggio ricevuto sia quello originale e che non vi siano state alterazioni nel mezzo

Se la città intercetta il messaggero, può modificarlo, ma ciò renderebbe il nonce non valido per la suddetta regola. Per esempio, se il messaggio diviene “Attaccare alle 12.00!102654”, allora se il generale B eseguisse l’hash di questo messaggio, otterrebbe:

f2aaeaa4896e5d023d07c60858b9a7e4d20d4f495b06786d4d2ec739fd16d339

Questo non rispetta il criterio dei 4 zeri iniziali. Saprebbe quindi che il messaggio è stato alterato e non lo prenderebbe in considerazione.

Certo la città potrebbe modificare il messaggio e ricalcolare l’hash, ma impiegherebbe del tempo, e in quel frangente un altro messaggero potrebbe essere stato inviato tra i generali con informazioni più nuove e aggiornate.

Questa esemplificazione ha lo scopo di chiarire il concetto. Nei prossimi articoli affronteremo in modo più dettagliato il discorso del POW e di come questo sistema aiuti a garantire la sicurezza dei sistemi basati su Blockchain.

Questo tool permette di replicare lo stesso esercizio che abbiamo fatto utilizzato come esempio. Arrivati a questo punto potrebbe essere molto interessante sperimentare con le tue mani la verifica del Nonce per non rimanere sul teorico ma fare anche un po’ di pratica
https://emn178.github.io/online-tools/sha256.html

Merkle Tree

Il nome Merkle Tree è in uso dal 1979, anno in cui Ralph Merkle ne depositò il brevetto, ed indica, nelle computer science, un albero di hash, cioè un albero binario in cui ogni nodo è identificato dall’hash dei suoi nodi figli.

Questo genere di strutture dati consente di riassumere e verificare in modo molto efficiente l’integrità di grandi set di dati, eseguendo un numero molto ridotto di operazioni. Per convenzione l’albero viene disegnato capovolto, con le “radici” in alto e le “foglie” in basso.

Immaginiamo di avere 16 blocchi di dati, da A a P. Vogliamo realizzare un Merkle Tree che ci consenta di poter verificare in modo rapido l’integrità di qualsiasi blocco senza dover riscaricare l’intera struttura.

Per far questo prendiamo uno ad uno tutti i blocchi di dati e ne calcoliamo l’hash, utilizzando una delle funzioni di hashing esistenti.

Ricordiamo come nota, che una funzione di hash è una funzione matematica che dato un set di dati di qualsiasi lunghezza in ingresso, genera come uscita una stringa di lunghezza fissa predeterminata.

Per questo esempio immaginiamo di utilizzare un double-SHA256 (SHA256 ripetuto 2 volte), stesso metodo utilizzato nei merkle tree di bitcoin.

Calcoliamo quindi gli hash di ogni blocco e otteniamo un gruppo di hash H_A-H_P. Reiteriamo il calcolo dell’hash, prendendo a coppie gli hash appena generati:

H_AB = SHA256(SHA256(H_A-H_P));

H_CD = SHA256(SHA256(H_C-H_D));

…

H_OP = SHA256(SHA256(H_O-H_P));

Abbiamo quindi ottenuto 8 nuovi hash dai precedenti 16, risalendo quindi di un livello. Reiteriamo nuovamente i calcoli fino ad ottenere un unico hash denominato Merkle Root, che rappresenta la radice dell’albero, ossia l’hash che descrive l’intero contenuto della struttura dati: H _{ABCDEFGHIJLKMNOP.}

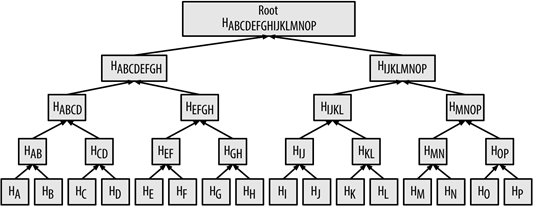
Qualsiasi modifica, anche minima, in uno dei blocchi della struttura causerà un cambiamento radicale del merkle root ed indicherà, appunto, una corruzione nei dati.

Data la struttura precedente, vediamo quali operazioni sarebbero necessarie per verificare se il contenuto del blocco K sia stato alterato o meno.

Il blocco K ha come hash H_K. Risalendo l’albero dobbiamo ricalcolare H_KL, H_IJKL, H_IJKLMNOP e la merkle root, indicati con contorno tratteggiato nello schema seguente. Per questi calcoli abbiamo bisogno unicamente dei dati del blocco L degli hash H_L, H_IJ, H_MNOP, H_ABCDEFGH, indicati in blu nello schema.

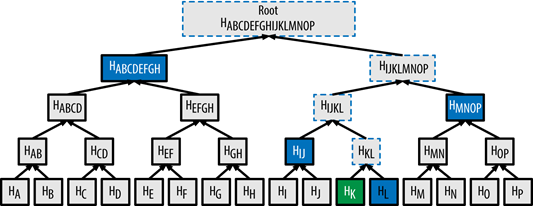
Il vantaggio è evidente. Abbiamo avuto bisogno unicamente di una piccola frazione dei dati della struttura per verificare se uno dei blocchi sia stato o meno alterato. Questo si trasforma in un minore utilizzo di banda e in un minore utilizzo delle risorse computazionali necessarie per effettuare le verifiche.

Con questo articolo si conclude il nostro percorso alla scoperta delle tecnologie e metodologie di base di bitcoin e delle criptovalute in generale.

A partire dal prossimo articolo cominceremo ad approfondire Bitcoin esaminando peculiarità e modi di funzionamento.